| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 자료구조
- 스택
- heap
- 스터디
- 거품정렬
- 선택정렬
- 해시함수
- divide and conquer
- 큐
- 프로그래머스
- 파싱
- 퀵정렬
- 힙
- 코테준비
- LinkedList
- 백준
- 15552번
- 코테
- 팀정렬
- 이진트리탐색
- 분할정복
- 우선순위 큐
- 트라이
- 삽입정렬
- collections.sort
- MSA
- 코딩테스트
- stack
- Timsort
- 연결리스트
- Today
- Total
Little bIT awesome
[2주차] Computer Architecture(2/2) 본문
고정 소수점 & 부동 소수점
1. 고정 소수점(Fixed Point)
소수점이 찍힐 위치를 미리 정해놓고 소수를 표현하는 방식 (정수 + 소수)
ex) -3.141592는 부호(-1), 정수부(3), 소수부(0.141592), 3가지 요소로 이루어짐

- 장점 : 실수를 정수부와 소수부로 표현하여 단순하다.
- 단점 : 표현의 범위가 너무 적어서 활용하기 힘들다(정수부는 15bit, 소수부는 16bit) → 정밀도가 낮다
2. 부동 소수점(Floating Point)
실수를 가수부 + 지수부로 표현한다.
- 가수 : 실수의 실제값 표현
- 지수 : 크기를 표현함. 가수의 어디쯤에 소수점이 있는지 나타냄
지수의 값에 따라 소수점이 움직이는 방식을 활용한 실수 표현 방법(소수점의 위치가 고정되어 있지 않다)
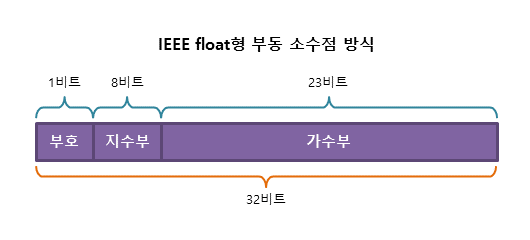
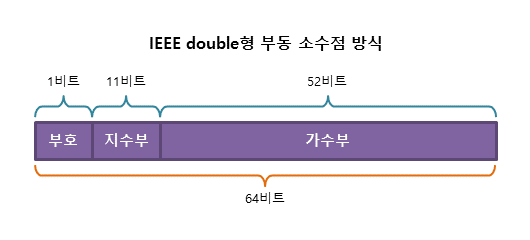
- 장점 : 표현할 수 있는 수의 범위가 넓어진다. (현재 대부분 시스템에서 활용 중 ex. Java와 C의 float, double, long double)
- 단점 : 오차가 발생할 수 있다. (부동소수점으로 표현할 수 있는 방법이 매우 다양함)
100000111.010011001100110...(263.3)을 2진수 부동 소수점 방식으로 변환하는 법
1바로 뒤로 소수점을 옮겨서 표현하도록 변환
→ 1.00000111010011001100110... * 2^8 으로 표현됨
이 때 8을 지수라고 하고 127 + 8을 (IEEE 표준 방식) 지수부에 기록
소수점 이후 숫자열 전체를 가수라고 하고 가수부에 기록
- 부호 비트: 0
- 지수 비트: 10000111 (127 + 8 = 135)
- 가수 비트: 00000111010011001100110
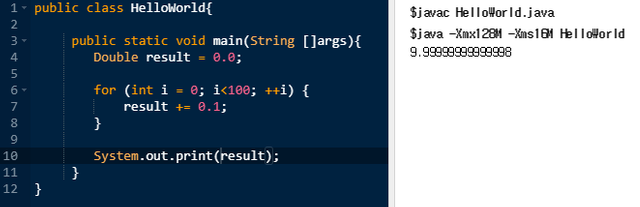
부동 소수점의 오류
0.1을 정확히 표현할 수 없기 때문에 0.1을 100번 더해도 10이 나오지 않음
패리티 비트 & 해밍 코드
패리티 비트
정보 전달 과정에서 오류가 생겼는지 검사하기 위해 추가하는 비트
전송하고자 하는 데이터의 각 문자에 1비트를 더하여 전송한다.
종류 : 짝수, 홀수
※ 짝수 패리티일 때, 7비트 데이터가 1010001라면?
1이 총 3개이므로, 짝수를 맞춰주기 위해 1을 더해야 함.
답 : 11010001 (맨 앞이 패리티비트라면)
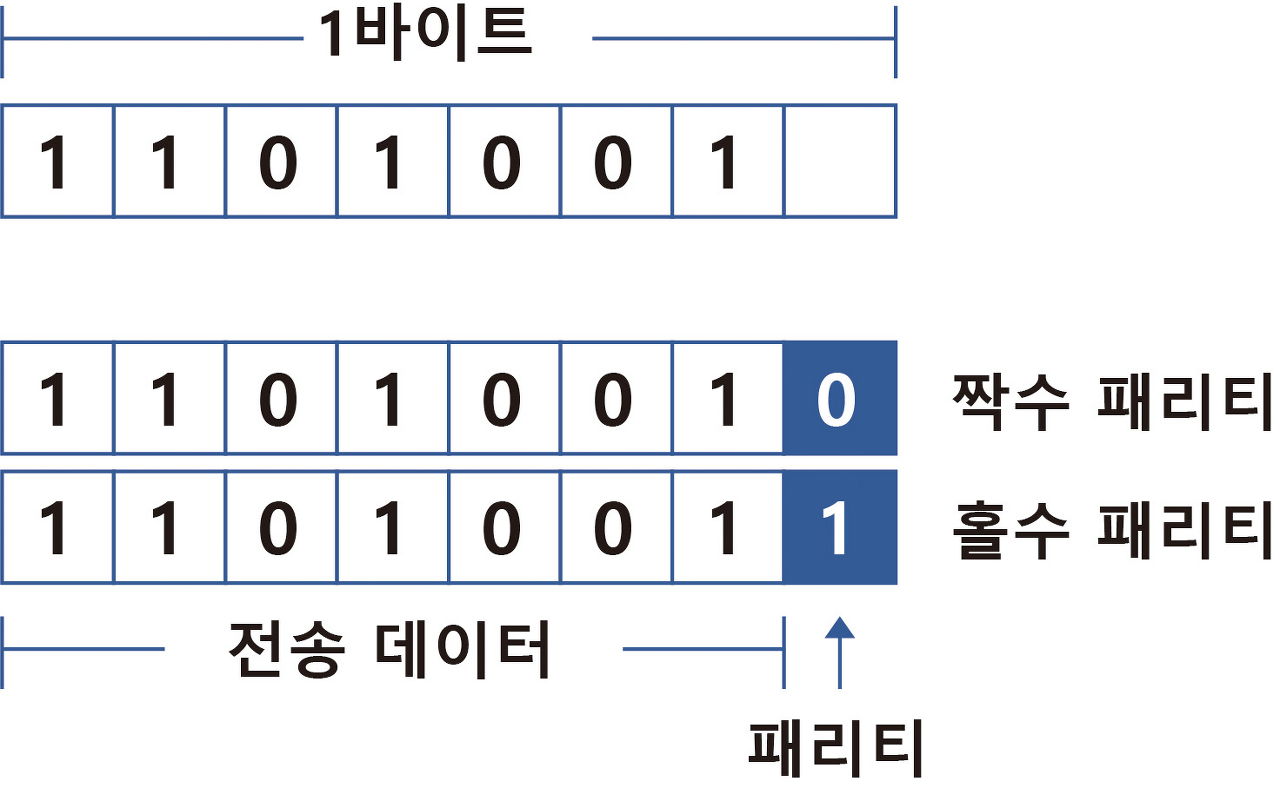
1바이트 구조에서 7비트 크기의 ASCII 코드를 제외한 나머지 1비트이다.
패리티 비트 작동 방식
120을 8비트 공간에 저장하면 다음과 같이 저장됨

이 상태에서 오류가 발생하여 첫번째 1이 0으로 바뀐다면 56으로 원하지 않는 데이터가 됨

이 데이터에 짝수 패리티 비트를 적용해보자.
데이터의 합이 짝수가 되게 만들어야 하므로 맨 뒤 패리티 비트는 0이 된다.

이 상태에서 첫번째 1이 오류로 소실되더라도 패리티를 포함한 데이터의 합은 짝수이기 때문에
소실된 데이터가 1이라는 것을 예측할 수 있다.

단, 오류로 2개의 비트가 소실될 경우 검출할 수 없다는 한계를 가짐
해밍 코드
데이터 전송 시 1비트의 에러를 정정할 수 있는 자기 오류정정 코드
패리티비트를 보고, 1비트에 대한 오류를 정정할 곳을 찾아 수정할 수 있다.
(패리티 비트는 오류를 검출하기만 할 뿐 수정하지는 않기 때문에 해밍 코드를 활용)
해밍 코드 생성 규칙

2의 n승 번째 자리인 1, 2, 4번째 자릿수가 패리티 비트
if 비트 수(m)가 8이라면, 추가되는 패리티 비트의 수(P)는 4

pn의 패리티체킹 범위는 pn부터 시작하여 n개의 비트를 포함하고 n개의 비트를 건너 뜀
p1 : 1, 3, 5, 7, 9, 11 ..
p2 : 2, 3, 6, 7, 10, 11 ..
p4 : 4, 5, 6, 7, 12 ..
p8 : 8, 9, 10 ..
짝수 패리티의 해밍코드가 0011011일 때, 오류가 수정된 코드는?
1. 1, 3, 5, 7번째 비트 확인 : 0101로 짝수이므로 0
2. 2, 3, 6, 7번째 비트 확인 : 0111로 홀수이므로 1
3. 4, 5, 6, 7번째 비트 확인 : 1011로 홀수이므로 1
110 = 6
6번째 비트를 수정하면 된다.
따라서, 0011001
ARM 프로세서
프로세서란? 메모리에 저장된 명령어들을 실행하는 유한 상태 오토마톤
ARM : Advanced RISC Machine
진보된 RISC 기기의 약자로 ARM의 핵심은 RISC
RISC : Reduced Instruction Set Computing (감소된 명령 집합 컴퓨팅)
단순한 명령 집합을 가진 프로세서가 복잡한 명령 집합을 가진 프로세서보다 훨씬 더 효율적이지 않을까? 라는 의문에서 탄생
ARM 구조

ARM은 칩의 기본 설계 구조만 만들고, 실제 기능 추가와 최적화 부분은 개별 반도체 제조사의 영역으로 맡긴다.
따라서, 물리적 설계는 같아도, 명령 집합이 모두 다르기 때문에 서로 다른 칩이 되기도 하는 것이 ARM
소비자에게는 칩이 논리적 구조인 명령 집합으로 구성되면서, 이런 특성 때문에 물리적 설계 베이스는 같지만
용도에 따라 다양한 제품군을 만날 수 있는 특징이 있다.
아키텍처는 논리적인 명령 집합을 물리적으로 표현한 것이므로, 명령어가 많고 복잡해질수록 물리적인 칩 구조도 크고 복잡해짐
(기존의 x86CPU CISC(Complex Instruction Set Computer) 아키텍쳐로 명령어가 많다)
하지만, ARM은 RISC 설계 기반으로 '단순한 명령집합을 가진 프로세서가 복잡한 것보다 효율적'임을 기반하기 때문에
명령 집합과 구조가 단순함
따라서 ARM 기반 프로세서가 더 작고, 효율적이며 상대적으로 느린 것
단순한 명령 집합은, 적은 수의 트렌지스터만 필요하므로 간결한 설계와 더 작은 크기를 가능하게 한다.
반도체 기본 부품인 트랜지스터는 전원을 소비해 다이의 크기를 증가시키기 때문에
스마트폰이나 태블릿PC, IoT를 위한 프로세서에는 가능한 적은 트랜지스터를 가진 것이 이상적임(작은 다이 사이즈로 설계됨)
따라서, 명령 집합의 수가 적기 때문에 트랜지스터 수가 적고 이를 통해 크기가 작고 전원 소모가 낮은 ARM CPU가 많이 사용됨
ARM의 장점은?
소비자에 있어 ARM은 '생태계'의 하나라고 생각할 수 있다.
ARM을 위해 개발된 프로세서는 오직 ARM 프로세서가 탑재된 기기에서만 실행할 수 있다.
(즉, x86 CPU 프로세서 기반 프로그램에서는 ARM 기반 기기에서 실행할 수 없음)
따라서 ARM에서 실행되던 프로그램을 x86 프로세서에서 실행되도록 하려면 (혹은 그 반대로) 프로그램에 수정이 가해져야만 한다.
하지만, 하나의 ARM 기기에 동작하는 OS는 다른 ARM 기반 기기에서도 잘 동작한다.
이러한 장점 덕분에 수많은 버전의 안드로이드가 탄생하고 있으며
또한 HP나 블랙베리의 태블릿에도 안드로이드가 탑재될 수 있는 가능성이 생기게 된 것이다.
(하지만 애플사는 iOS 소스코드를 공개하지 않고 있기 때문에 애플 기기는 불가능하다)
ARM을 만드는 기업들은 통해 전력 소모를 줄이고 성능을 높이기 위해 설계를 개선하며 노력하고 있다.
'CS 공부 > Computer Science' 카테고리의 다른 글
| [네트워크] DNS 동작방식 (0) | 2024.10.29 |
|---|---|
| [1주차] Computer Architecture(1/2) (0) | 2023.09.29 |


