[Week10] MST 알고리즘(2) - Prim's Algorithm

MST (Minimum Spanning Tree)

그래프 이론에서 사용되며, 주어진 가중치 그래프에서 최소 비용으로 모든 정점을 연결하는 트리를 찾는 알고리즘

네트워크 설계, 전력 배선, 클러스터링 등 다양한 분야에서 활용된다. 

 

여러가지 MST 알고리즘이 있지만, 그 중에서도 가장 널리 사용되는 두 가지 알고리즘

1. Kruskal's Algorithm (크루스칼 알고리즘)

2. Prim's Algorithm (프림 알고리즘)

https://littlebitawesome.tistory.com/entry/Week10-MSTMinimum-Spanning-Tree-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

[Week10] MST 알고리즘(1) - Kruskal's Algorithm

 

Prim's Algorithm (프림 알고리즘)

시작 정점에서 정점을 추가해가며 단계적으로 트리를 확장하는 알고리즘

매 순간 최선의 조건을 선택하는 그리디 알고리즘을 바탕에 둔다.

즉, 탐색 정점에 대해 연결된 인접 정점들 중 비용이 가장 적은 간선으로 연결된 정점을 선택한다. 

 

프림 알고리즘의 과정

1. 임의의 시작 정점 선택

임의의 시작 정점을 선택하여 시작

 

2. 트리 확장

현재 MST 집합과 연결된 간선 중 가장 작은 가중치를 가진 간선을 선택하여 MST 집합에 추가한다.

 

3. 사이클 방지

선택한 간선이 사이클을 형성하지 않도록 한다.

 

4. 모든 정점을 포함할 때까지 반복

MST 집합이 모든 정점을 포함할 때까지 위 과정을 반복한다.

 

 

예시

위 그래프의 최소 신장 트리를 프림 알고리즘으로 구해보자. 시작 정점은 A라 한다. 

 

A와 인접한 노드 B, C 중 C가 가장 가중치가 낮은 간선으로 연결되어 있으니 C를 집합에 넣고 비용에 AC 가중치를 더한다.

 

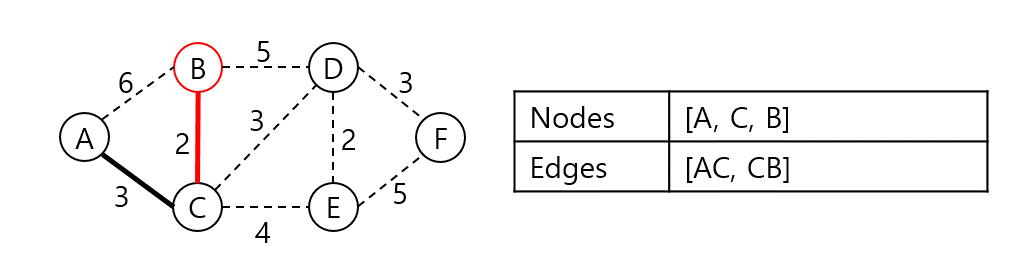
A, C와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 B다. 집합에 B를 넣고 CB 가중치를 더한다.

 

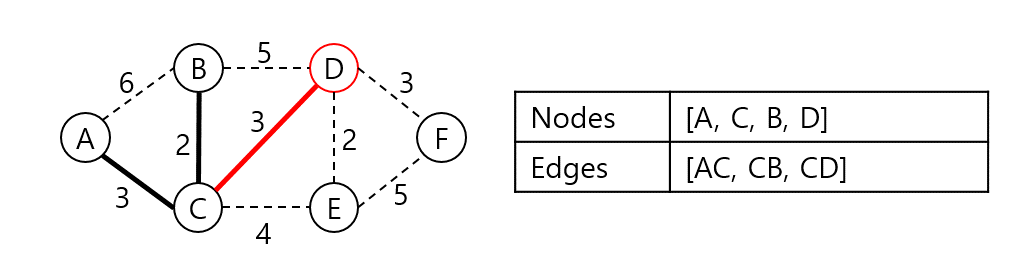
A, C, B와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 D다. 집합에 D를 넣고 CD 가중치를 더한다.

 

A, C, B, D와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 E다. 집합에 E를 넣고 DE 가중치를 더한다.

 

A, C, B, D, E와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점 F를 집합에 넣고 DF 가중치를 더한다.

트리의 집합에 속한 원소의 개수가 N이 되었으므로 탐색을 중단한다.

탐색 결과 최소 신장 트리 구축의 비용은 13으로 확인되었다.

 

구현 코드

class Edge implements Comparable<Edge>{
	int w;
	int cost;
	
	Edge(int  w, int cost){
		this.w = w;
		this.cost = cost;
	}
	
	@Override
	public int compareTo(Edge o) {
		return this.cost - o.cost;
	}
}

public class prim_main {
	static List<Edge>[] graph;
	
	public static void prim(int start, int n) {
		boolean[] visit = new boolean[n + 1];
		
		PriorityQueue<Edge> pq = new PriorityQueue<>();
		pq.offer(new Edge(start, 0));
		
		int total = 0;
		while(!pq.isEmpty()) {
			Edge edge = pq.poll();
			int v = edge.w;
			int cost = edge.cost;
			
			if(visit[v]) continue;
            
			visit[v] = true;
			total += cost;
			
			for(Edge e : graph[v]) {
				if(!visit[e.w]) {
					pq.add(e);
				}
			}
		}
		System.out.println(total);
	}

	
	public static void main(String[] args) throws IOException {
   		// 그래프 입력, 저장
		BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
		int n = Integer.parseInt(bf.readLine());
		int m = Integer.parseInt(bf.readLine());
		
        // 그래프 선언, 간선 리스트로 표현
		graph = new ArrayList[n + 1];
		for (int i = 0; i < graph.length; i++) graph[i] = new ArrayList<>();
		
		StringTokenizer st;
		for (int i = 0; i < m; i++) {
			st = new StringTokenizer(bf.readLine());
			int v = Integer.parseInt(st.nextToken());
			int w = Integer.parseInt(st.nextToken());
			int cost = Integer.parseInt(st.nextToken());
			
			graph[v].add(new Edge(w, cost));
			graph[v].add(new Edge(v, cost));
		}
		
        // 프림 알고리즘 수행
		prim(1, n);
	}
}

 

https://velog.io/@suk13574/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98Java-%ED%94%84%EB%A6%BCPrim-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

[알고리즘/Java] 프림(Prim) 알고리즘

https://8iggy.tistory.com/159

프림 알고리즘(Prim's Algorithm)