| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 15552번
- 우선순위 큐
- 퀵정렬
- 코테
- 해시함수
- 트라이
- 백준
- 프로그래머스
- 선택정렬
- 힙
- 자료구조
- 스택
- 거품정렬
- Timsort
- MSA
- 분할정복
- 파싱
- 코테준비
- heap
- 코딩테스트
- stack
- 연결리스트
- 스터디
- 삽입정렬
- divide and conquer
- LinkedList
- 이진트리탐색
- 큐
- 팀정렬
- collections.sort
- Today
- Total
Little bIT awesome
[week4] 백트래킹(Backtracking) 알고리즘 본문
백트래킹
재귀적으로 문제를 하나씩 풀어나가되
현재 재귀를 통해 확인 중인 상태(노드)가 제한 조건에 위배되는지 판단하고
그러한 경우에 해당 상태(노드)를 제외하고 다음 단계로 나아가는 방식이다.
더 이상 탐색할 필요가 없는 상태(노드)를 제외하는 것을 가지치기(Pruning)라고도 한다.
즉, 이 방법을 통해 우리는 모든 경우의 수를 체크 하지 않고 필요한 것만 체크하여 전체 풀이 시간을 단축할 수 있게 된다!
백트래킹을 사용해 해결할 수 있는 문제는 의사결정, 최적화, 열거하기 등의 경우가 있다.
사실 백트래킹은 사용 가능한 경우가 많지만 시간복잡도가 보통 Exponential(지수, 2� 꼴)이며,
대부분 Dynamic Programming, 그리디 알고리즘 등으로 더 빠르게 해결할 수 있다.
하지만 일부 경우의 문제들은 여전히 백트래킹으로만 해결이 가능한 문제도 있으며 그러한 경우에 많이 사용된다.
백트래킹 사용 예시
N-Queen 문제를 통해 백트래킹을 이해해보자
N-Queen은 N개의 체스 퀸을 N x N 크기의 체스보드에서 움직이되 상호 공격을 하지 않도록 움직이는 방법이다.

이를 정답으로 표시한다면 4 x 4 배열에 퀸의 위치는 1로, 나머지는 0으로 표시한다면 정답이 될 것이다.
어떻게 해결할 수 있을까?
1. 우선, 제일 좌측 열에서 시작하여 하나씩 비교하여 해당 열의 모든 칸에 퀸이 이미 배치되었는지 체크한다.

2. 해당 열에 퀸이 없다면 우선 그 캍을 유망한 후보로 고르고, 해당 행 전체를 조사하여 퀸이 배치되었는지 조사한다.
예를 들어 0 x 0 의 위치를 유망하다고 본다면 아래와 같이 체크한다.

3. 행 또한 체크를 완료했다면, 대각선으로 체크하여 퀸이 배치된 내역이 있는지 확인한다. 아래 그림과 같다.

4. 이를 통해 모두 비어 있다면 해당 위치에 퀸을 놓고 다음 열에서도 동일하게 체크를 수행한다.
이를 통해 3번 째 열까지 체크하면 다음과 같이 퀸이 배치될 것이다.

위에서와 같이, 3번째 열에서는 어떠한 곳에도 퀸을 배치할 수 없게 된다.
그러니 백트래킹을 통해 해당 칸을 제외하고 2번째 열로 돌아가 퀸을 다시 배치하게 된다.
5. 위 과정을 반복하여 전체 퀸을 모든 열에 놓을 수 있는 경우를 찾을 때까지 반복한다.
(재귀 + 반복문 기반 백트래킹 사용)
위의 예시는 아래와 같은 정답을 얻을 수 있다.

예시 코드
public class NQueen{
static int N = 4;
static int[][] board = new int[4][4];
public static void main(String[] args){
if(put_queen(0) == false){
System.out.println("Solution does not exist!");
} else {
for(int i=0; i < N; i++){
for(int j=0; j < N; j++){
System.out.print(board[i][j] + ", ");
}
System.out.println();
}
}
}
// 재귀와 반복을 통해 문제를 해결하는 메소드(각 컬럼에 대해 체크)
private static boolean put_queen(int col){
// N보다 열의 숫자가 높거나 같다면 모든 열에 퀸이 배치된 상태를 의미
if(col >= N) return true;
// 현재 열(Column)에서 각 행을 하나씩 체크한다.
for(int i=0; i < N; i++){
// 현재 열의 i번째 행에 퀸을 위치시킬 수 있는지 파악
if(check(i, col) == true){
board[i][col] = 1;
// 위치 시켰으면, 이후 열에 대해서도 연속적으로 가능한지 확인!
if(put_queen(col+1) == true){
return true;
}
// 만약 이후 열에 대해서 true 반환이 안되었다면 다시 0으로 수행하고
// 백트래킹을 통해 다음 row로 넘어가서 수행
board[i][col] = 0;
}
}
// true를 이전에 반환 못했다면 답이 없는 것이므로 false 반환
return false;
}
// 현재 행/열에 퀸이 이미 배치된 상태인지 확인하는 메소드
private static boolean check(int row, int col){
int i,j;
// 현재 행의 모든 열에 퀸이 있는지 테스트
for(i = 0; i < col; i++){
if(board[row][i] == 1){
return false;
}
}
// 현재 위치의 좌상단 대각선으로 퀸이 있는지 테스트
for(i = row, j = col; i >= 0 && j >= 0; i--, j--){
if(board[i][j] == 1){
return false;
}
}
// 현재 위치의 우하단 대각선으로 퀸이 있는지 테스트
for(i = row, j = col; i < N && j >= 0; i++, j--){
if(board[i][j] == 1){
return false;
}
}
return true;
}
}
깊이 우선 탐색 - DFS
백트래킹을 사용하는 알고리즘 중 하나는 대표적으로 DFS가 있다.
DFS는 재귀를 통해 가능한 경로 중 유망한 경로만 찾아서 탐색을 수행한 뒤 다시 돌아와 그 중 가장 최적의 경로를 반환한다.
트리 구조의 순회와 비슷한 방식으로 동작한다고 보면 되는데,
최초 시작 정점에서 가장 먼저 이어져 있는 (간선으로 연결된) 정점을 하나 찾고
해당 정점에 또 인접한 정점을 찾아 더 이상 깊이 갈 수 없을 때까지 탐색한 뒤 돌아오는 방식이다.
트리와의 큰 차이점은, 그래프는 순환(Cycle)할 수 있다는 것이다.
그래서, 순환 탐지(Cycle Detection)를 할 수 있도록 추가적인 기능을 구현해야 한다.
BFS(너비 우선 탐색)와의 큰 차이점은, DFS는 탐색을 한 뒤 이전의 정점으로 돌아온다는 것이다.
이것을 백트래킹이라고 하며 이를 이용하여 다양한 문제에 활용할 수 있다.
그림으로 알아보기

위의 애니메이션을 보면,
0 → 1 → 2 로 이동한 뒤 2에서 더 이상 깊이 갈 수 없어 2를 탐색 완료 후, 1로 돌아온다.
다시 1 → 3 → 4로 더 깊이 들어갔다가 나오는 방식을 반복한다.
말 그대로, 깊이 갈 수 있을 때까지 탐색하고 더 이상 탐색이 불가하면 되돌아오는 방식이다.
DFS 사용 예시
그래프의 순환이 있는지 확인하는 경우 많이 쓰인다. BFS로도 가능하지만 DFS가 더 메모리 효율적이다.
기타 경로 찾기, 위상 정렬, 미로 찾기 등 다양한 예시에 사용될 수 있다.
하지만 최단 경로를 찾을 때는 DFS 보다는 BFS를 기반으로 탐색해야 한다.
BFS는 최단 경로를 즉각적으로 보장해주면서 탐색을 할 수 있지만, DFS는 그렇지 못한 경우가 있기 때문이다.
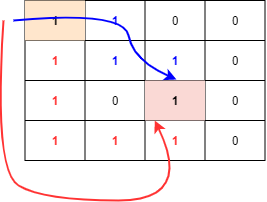
만약 주황색으로 칠해진 곳에서 빨간색으로 칠해진 곳으로 가고자 할 때,
파란 화살표로 가는 경로와 빨간 화살표로 가는 경로가 있다.
BFS로 탐색하게 되면, 빨간 부분, 파란 부분 인접 정점을 통시에 차례대로 탐색을 하게 된다.
또한, 시작점이 고정이라 무조건 모든 인접 정점이 최소인 경로로만 이동하도록 보장된다.
DFS로 탐색하게 되면, 빨간색 부분부터 우선 탐색이 이루어진다.
하지만, 이 경로는 최소 경로라는 보장이 불가능하다.
(실제 예시에서 볼 수 있듯이 이는 최소 경로가 아니다!)
보장을 하기 위해서는 이미 방문한 경로의 정점을 미방문 상태로 전환하고 다른 모든 동일 위치에 도달할 수 있는 경우를 체크해야 한다.
그런데 이 방식은 DFS가 아니라 Brute Force 방식이 된다. (DFS, BFS는 기본적으로 이미 방문한 정점을 다시 방문하지 않아야 한다)
그러면 문제를 푸는데, 시간복잡도가 높아져 문제를 풀 수 없다.
구현 방법
스택 또는 재귀 방식을 이용하여 구현할 수 있다.
스택은 FILO(First-In, Last-Out) 방식이기 때문에
인접한 정점이 우선이 아닌 더 멀리 있는 정점을 우선 탐색한 뒤 돌아올 수 있다.
재귀 자체가 내부적으로 Stack을 사용하는 방식이기 때문에 재귀 방식으로 진행하는 것 또한 가능하다.
둘 중에서는 재귀 방식이 더 많이 쓰인다. 더욱 구현이 간단하기 때문이다.
복잡도
시간 복잡도 : O(V+E), V는 정점 / E는 간선의 개수로 그 개수에 따라 전체 탐색에 시간이 소요된다.
공간 복잡도 : O(V), 최악의 경우, 정점이 1열로 잉어져 전체 정점의 수 만큼 스택이 쌓일 수 있다.
코드
pacakge com.test;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Stack;
public class Graph {
public static void main(String[] args){
Graph g = new Graph(6);
g.addEdge(0, 1); // 0 -> 1 연결
g.addEdge(0, 5); // 0 -> 5 연결
g.addEdge(1, 2); // 1 -> 2 연결
g.addEdge(1, 3); // 1 -> 3 연결
g.addEdge(1, 4); // 1 -> 4 연결
g.addEdge(2, 0); // 2 -> 0 연결
g.addEdge(3, 4); // 3 -> 4 연결
g.addEdge(4, 2); // 4 -> 2 연결
g.dfs();
}
private int v; // 정점의 개수
private LinkedList<Integer> adj[]; // 인접 리스트
public Graph(int v){
this.v = v;
this.adj = new LinkedList[v];
for(int i=0; i < v; i++){
adj[i] = new LinkedList<>();
}
}
// Source 정점에서 Dest 정점을 이어주는 메소드
public void addEdge(int s, int d){
this.adj[s].add(d);
}
// DFS를 수행하는 메소드
public void dfs(){
// 전체 정점이 최초에는 visited를 false 설정
boolean visited[] = new boolean[this.v];
// 반복문 기반으로 Disconnected Graph라도 전체 탐색이 가능
// 재귀 기반 DFS 수행 시작
for(int i=0; i < this.v; i++){
if(!visited[i]){
dfs_recurvise(i, visited);
}
}
System.out.println();
// 스택 기반 수행을 위해 다시 false로 초기화
visited = new boolean[this.v];
// 스택 기반 DFS 수행 시작
for(int i=0; i < this.v; i++){
if(!visited[i]){
dfs_stack(i, visited);
}
}
}
// DFS 재귀 수행 메소드
public void dfs_recurvise(int v, boolean visited[]){
visited[v] = true;
System.out.print(v + " ");
// 방문하지 않은 인접 정점을 모두 찾아 우선 탐색 수행
Iterator<Integer> i = this.adj[v].listIterator();
while(i.hasNext()){
int n = i.next();
if(!visited[n]){
dfs_recurvise(n, visited);
}
}
}
// DFS 스택 수행 메소드
public void dfs_stack(int start, boolean visited[]){
Stack<Integer> stack = new Stack<>();
stack.push(start);
while(!stack.isEmpty()){
int v = stack.pop();
System.out.print(v + " ");
// 방문하지 않은 인접 정점을 모두 찾아 우선 탐색 수행
Iterator<Integer> i = this.adj[v].listIterator();
while(i.hasNext()){
int n = i.next();
if(!visited[n]){
visited[n] = true;
stack.push(n);
}
}
}
}
}
/*결과
0 1 2 3 4 5
0 5 1 4 3 2
Process finished with exit code 0
결과가 아래가 다른 이유는 print 시점 때문
재귀는 탐색 시에 print하고 스택 시에는 stack에서 뺄 때 print함
중요한 것은 모든 것이 탐색 되느냐로 본다.
*/
https://hongjw1938.tistory.com/88
알고리즘 - 백트래킹(Backtracking)
1. 백트래킹이란? 백트래킹은 알고리즘 기법 중 하나로, 재귀적으로 문제를 하나씩 풀어나가되 현재 재귀를 통해 확인 중인 상태(노드)가 제한 조건에 위배되는지(유망하지 않은지) 판단하고 그
hongjw1938.tistory.com
https://hongjw1938.tistory.com/42?category=909529
알고리즘 - 그래프 탐색(깊이 우선 탐색 - DFS)
이번 포스팅에서는 그래프 자료구조의 탐색에 대해서 알아보자. 이전 포스팅에서 배열 / 리스트 형태의 자료구조에 대한 탐색 방법을 알아보았으니 관련 포스팅은 아래 링크를 참고 배열 / 리스
hongjw1938.tistory.com
'코딩테스트 > 알고리즘 정리' 카테고리의 다른 글
| [week5] DFS 와 BFS (0) | 2024.03.19 |
|---|---|
| Brute-Force, 백트래킹, DFS (1) | 2024.03.15 |
| [Week3] 분할 정복 (Divide and Conquer) (0) | 2024.02.16 |
| [Week3] 이분 탐색 (Binary Search) (0) | 2024.02.15 |
| Collections.sort에 쓰이는 TimSort (0) | 2024.02.02 |



