| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 퀵정렬
- 프로그래머스
- stack
- 거품정렬
- 삽입정렬
- 해시함수
- 분할정복
- 스터디
- collections.sort
- Timsort
- 우선순위 큐
- 스택
- 트라이
- 코딩테스트
- 15552번
- divide and conquer
- 파싱
- 연결리스트
- 팀정렬
- LinkedList
- MSA
- 백준
- 자료구조
- 큐
- 힙
- 코테준비
- 코테
- 이진트리탐색
- heap
- 선택정렬
- Today
- Total
Little bIT awesome
[week7] 최장 증가 부분 수열(LIS) 알고리즘 본문
최장 증가 부분 수열(LIS, Longest Increasing Subsequence)

원소가 n개인 배열의 일부 원소를 골라내서 만든 부분 수열 중,
각 원소가 이전 원소보다 크다는 조건을 만족하고,
그 길이가 최대인 부분 수열을 최장 증가 부분 수열이라고 한다.
예를 들어 { 6, 2, 5, 1, 7, 4, 8, 3 } 이라는 배열이 있을 경우, LIS는 { 2, 5, 7, 8 } 이 된다.
{ 2, 5 }, { 2, 7 } 등 증가하는 부분 수열은 많지만 그 중에서 가장 긴 것이 { 2, 5, 7, 8 } 이기 때문
일반적으로 최장 증가 부분 수열의 길이가 얼마인지 푸는 간편한 방법은 DP를 이용하는 것

아래에서 length[i]는 i번째 인덱스에서 끝나는 최장 증가 부분 수열의 길이를 의미한다.
for (int k = 0; k < n; k++){
length[k] = 1;
for (int i = 0; i < k; i++){
if(arr[i] < arr[k]){
length[k] = max(length[k], length[i] + 1);
}
}
}
주어진 배열에서 인덱스를 한 칸씩 늘려가면서 확인한다.
그리고 내부 반복문으로 k보다 작은 인덱스들을 하나씩 살펴 보면서 arr[i] < arr[k]인 것이 있을 경우,
length[k]를 업데이트한다.
업데이트를 하는 기준은,
- i번째 인덱스에서 끝나는 최장 증가 부분 수열의 마지막에 arr[k]를 추가했을 때의 LIS 길이와,
- 추가하지 않고 기존의 length[k]의 값
둘 중에 더 큰 값으로 length[k] 값을 업데이트한다.
DP를 활용할 시 이중 반목문을 이용하기 때문에 O(n^2)의 시간 복잡도를 가진다.
입력 값의 크기가 작을 경우 유용하다.
이분 탐색을 활용하여 LIS를 구현하기도 한다.
O(logn)의 시간 복잡도를 가진다. 때문에 입력 값의 크기가 클 경우 DP를 활용하는 경우보다 효율적이다.
다만, 이분 탐색을 활용하는 경우에는 정확한 LIS가 아닌 LIS의 길이를 구할 때 사용된다.
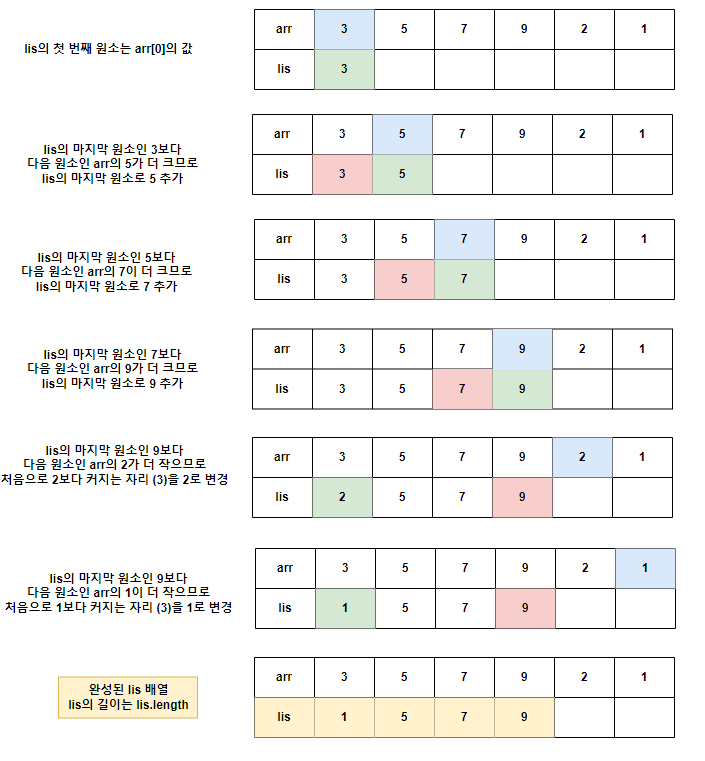
int[] lis = new int[size + 1]; // 가장 긴 증가하는 부분 수열. 가장 뒤에 있는 값은 부분 수열 중 가장 최댓값
int start = 0;
lis[start++] = arr[0]; // lis[start] 값을 arr[i]로 변경하고 1증가시킨다.
for (int i = 1; i < size; i++) {
// lis값의 맨 마지막 원소가 arr[i] 보다 작을 경우
if (lis[start - 1] < arr[i]) {
lis[start++] = arr[i]; // 해당 원소를 arr[i]값으로 변경하고 start를 1 증가 시킨다.
} else {
int end = 0;
while (start <= end) {
int mid = start + (end - start) / 2;
if (arr[mid] == arr[i]) {
return mid;
}
if (arr[mid] < arr[i]) {
start = mid + 1;
}
if (arr[mid] > arr[i]) {
end = mid - 1;
}
}
// start < end 일 경우 lis[start]의 값은 arr[i]의 값이 된다.
lis[start] = arr[i];
}
}
알고리즘 - 최장 증가 부분 수열(LIS) 알고리즘
컴퓨터/IT/알고리즘 정리 블로그
chanhuiseok.github.io
[알고리즘] LIS(최장 증가 부분 수열)이란 ?
LIS (Longest Increasing Subsequence) 최장 증가 부분 수열 최장 증가 부분 수열은 말 그대로 가장 길게 증가하는 부분 수열으로 즉, 어떤 수열에서 만들 수 있는 부분 수열 중에서 가장 길면서 오름차순을
hstory0208.tistory.com
'코딩테스트 > 알고리즘 정리' 카테고리의 다른 글
| [week9] 다익스트라 알고리즘 (Dijkstra Algorithm) (0) | 2024.04.30 |
|---|---|
| [week8] 그래프, 트리의 차이점 (0) | 2024.04.09 |
| [Week7] 동적 계획법 (DP: Dynamic Programming) (0) | 2024.04.02 |
| [week6] 그리디 알고리즘 (0) | 2024.03.26 |
| 인접 행렬과 인접 리스트 (0) | 2024.03.20 |




