인접 행렬과 인접 리스트

그래프를 구현하여 표현하는 방법에는 여러가지가 있지만 일반적으로 인접행렬과 인접리스트 방식이 있다. 

이 두가지 방식은 서로 정반대의 특징을 갖기 때문에 한 방식의 장점이 다른 방식의 단점이 되는 경우가 나타난다. 

따라서, 구현하려는 알고리즘, 그래프의 종류에 따라 적절하게 사용하여야 한다. 

 

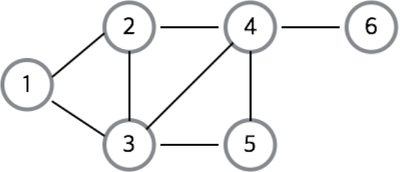
인접 리스트를 이용한 그래프 구현

package boj.study.week6;

import java.util.ArrayList;

public class adjacencyList {
    public static void main(String[] args) {
        int initSize = 6;
        ListGraph adjList = new ListGraph(initSize);

        adjList.put(1, 2);
        adjList.put(1, 3);
        adjList.put(2, 3);
        adjList.put(2, 4);
        adjList.put(3, 4);
        adjList.put(3, 5);
        adjList.put(4, 5);
        adjList.put(4, 6);

        adjList.printGraphToAdjList();

    }
}

// 그래프(리스트) 클래스
class ListGraph {
    private ArrayList<ArrayList<Integer>> listGraph;

    // 생성자
    public ListGraph(int initSize) {
        this.listGraph = new ArrayList<ArrayList<Integer>>();

        /**
         * 그래프 초기화
         * put(int x, int y) 에서 입력되는 정점의 값은 0 이상의 정수이나
         * ArrayList의 index는 0 부터 시작이므로
         * ArrayIndexOutOfBoundsException을 방지하기 위해
         * 정점을 담는 인접리스트의 size는 1을 더하여 초기화해줌
         * ex) initSize = 3
         * graph[0] -> 2 -> 3
         * graph[1] -> 1 -> 3 -> 4
         * graph[2] -> 1 -> 2 -> 4 -> 5
         * graph[3] -> 1 -> 2 -> 4 -> 5
         */
        for (int i = 0; i < initSize + 1; i++) {
            listGraph.add(new ArrayList<Integer>());
        }
    }

    public ArrayList<ArrayList<Integer>> getGraph() {
        return this.listGraph;
    }

    // 그래프 추가 (양방향)
    public void put(int x, int y) {
        listGraph.get(x).add(y);
        listGraph.get(y).add(x);
    }

    // 그래프 추가 (단방향)
    public void putSingle(int x, int y) {
        listGraph.get(x).add(y);
    }

    // 그래프 출력 (인접 리스트)
    public void printGraphToAdjList() {
        for (int i = 1; i < listGraph.size(); i++) {
            System.out.print("정점 " + i + "의 인접리스트");

            for (int j = 0; j < listGraph.get(i).size(); j++) {
                System.out.print(" -> " + listGraph.get(i).get(j));
            }
            System.out.println();
        }
    }
}

실행 결과

 

 

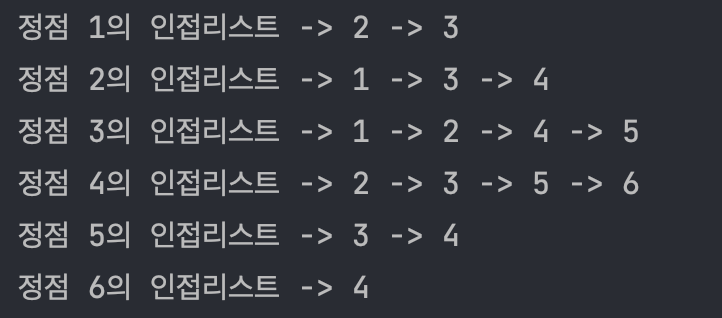
인접 행렬을 이용한 그래프 구현

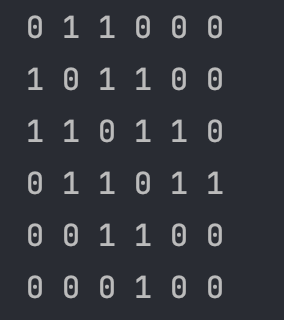
인접 행렬은 N x N 행렬로 graph[i][j]가 true라면 i에서 j로의 간선이 있다는 것을 의미

정점의 개수가 V라면 V^2 크기의 2차원 배열을 생성하여 1과 0을 사용하여 true / false를 구분하여 값을 저장한다. 

양방향 인접행렬의 경우 대칭 행렬의 형태로 구성된다. 

 

package boj.study.week6;

public class adjacencyArray {
    public static void main(String[] args) {
        int initSize = 6;
        ArrGraph adjArr = new ArrGraph(initSize);

        adjArr.put(1, 2);
        adjArr.put(1, 3);
        adjArr.put(2, 3);
        adjArr.put(2, 4);
        adjArr.put(3, 4);
        adjArr.put(3, 5);
        adjArr.put(4, 5);
        adjArr.put(4, 6);
        
        adjArr.printGraphToAdjArr();
    }
}

class ArrGraph {
    private int[][] arrGraph;

    public ArrGraph(int initSize) {
        /**
         * 그래프 초기화
         * put(int x, int y)에서 입력되는 정점의 값은 0 이상의 정수이나
         * 배열의 indexsms 0 부터 시작이므로
         * ArrayIndexOutOfBoundsException을 방지하기 위해
         * 정점을 담는 인접행렬의 행과 열 size는 1을 더하여 초기화 해줌
         */
        this.arrGraph = new int[initSize + 1][initSize + 1];
    }

    // 그래프 return
    public int[][] getGraph() {
        return this.arrGraph;
    }

    // 그래프 추가(양방향)
    public void put(int x, int y) {
        this.arrGraph[x][y] = this.arrGraph[y][x] = 1;
    }

    // 그래프 추가(단방향)
    public void putSingle(int x, int y) {
        this.arrGraph[x][y] = 1;
    }

    // 그래프 출력 (인접행렬)
    public void printGraphToAdjArr() {
        for (int i = 1; i < arrGraph.length; i++) {
            for (int j = 1; j < arrGraph[i].length; j++) {
                System.out.print(" " + arrGraph[i][j]);
            }
            System.out.println();
        }
    }
}

 

실행 결과

 

인접 행렬과 인접 리스트의 차이

	정점 간의 간선 여부	공간 복잡도
인접 행렬	정점 v1, v2에 대해 한 번의 접근으로 확인 가능	V개의 노드 표현을 위해 V^2 만큼의 공간이 필요 인접 노드를 찾기 위해선 모든 노드를 순회해야 함  공간복잡도 : O(V^2)
인접 리스트	리스트의 처음부터 하나씩 확인해야 함	V 개의 리스트에 간선 (E) 만큼 원소가 들어있음 인접 노드를 쉽게 찾을 수 있음 공간복잡도 : O(V + E)

 

인접 행렬과 인접 리스트가 사용되는 경우

인접 행렬 : 그래프에 간선이 많이 존재하는 밀집 그래프

인접 리스트 : 그래프에 간선이 적게 존재하는 희소 그래프

 

 

 

 

https://freestrokes.tistory.com/87

Java 인접행렬과 인접리스트를 이용하여 그래프 구현하기