| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- heap
- 코딩테스트
- collections.sort
- Timsort
- 프로그래머스
- 삽입정렬
- 코테준비
- 트라이
- 스택
- 연결리스트
- MSA
- 분할정복
- 코테
- 백준
- 큐
- 15552번
- 자료구조
- 이진트리탐색
- 거품정렬
- 힙
- 스터디
- LinkedList
- 우선순위 큐
- 파싱
- 해시함수
- divide and conquer
- stack
- 퀵정렬
- 팀정렬
- 선택정렬
- Today
- Total
Little bIT awesome
[5주차] Data Structure 3/4 (트리 & 이진 탐색 트리) 본문
Tree
Node와 Edge로 이루어진 자료구조

트리는 값을 가진 Node(vertex)와 이 노드를 연결해주는 Edge(link)으로 이루어진다.
노드에는 특정 정보를 저장할 수 있고, edge는 정보들간의 관계를 나타낸다.
제일 상위 노드를 Root(루트) 노드라고 한다. (그림 상 값 1을 가진 노드)
모든 노드들은 0개 이상의 자식 노드를 가지고 있으며 보통 부모-자식 관계로 부른다.
+
- path : edge에 의해 연결된 node들의 집합
- leaf 노드 : 자식이 없는 node
- subtree : 큰 tree에 속하는 작은 tree
- node의 degree : 각 노드가 지닌 가지의 수 (subtree의 개수)
- node level : 루트로부터 단순 경로의 길이

트리의 특징
1. 트리에는 사이클이 존재할 수 없다. (만약 사이클이 있으면 트리가 아니라 그래프)
2. 모든 노드는 자료형으로 표현이 가능하다.
3. 루트에서 한 노드로 가는 경로는 유일한 경로 뿐이다.
4. 노드의 개수가 N개면, 간선은 N-1개를 가진다.
가장 중요한 것은, '그래프와 트리의 차이가 무엇인가' 이다.
이는 사이클의 유무로 설명할 수 있다.
트리 순회 방식
트리를 순회하는 방식은 4가지가 있다.
1. 전위 순회 (pre-order)
2. 중위 순회 (in-order)
3. 후위 순회 (post-order)
4. 레벨 순회 (level-order)

1. 전위 순회 (pre-order)
각 루트를 순차적으로 먼저 방문하는 방식
(Root → 왼쪽 자식 → 오른쪽 자식)
1 → 2 → 4 → 8 → 9 → 5 → 10 → 11 → 3 → 6 → 13 → 7 → 14
2. 중위 순회 (in-order)
왼쪽 하위 트리를 방문 후 루트를 방문하고 오른쪽 하위 트리를 방문하는 방식
(왼쪽 자식 → Root → 오른쪽 자식)
8 → 4 → 9 → 2 → 10 → 5 → 11 → 1 → 6 → 13 → 3 →14 → 7
3. 후위 순회 (post-order)
왼쪽 하위 트리부터 하위를 모두 방문 후 루트를 방문하는 방식
(왼쪽 자식 → 오른쪽 자식 → Root)
8 → 9 → 4 → 10 → 11 → 5 → 2 → 13 → 6 → 14 → 7 → 3 → 1
4. 레벨 순회 (level-order)
루트 부터 계층별로 방문하는 방식
1 → 2 → 3 → 4 → 5 → 6 → 7 → 8 → 9 → 10 → 11 → 13 → 14
Code
// 제네릭 클래스 사용 -> 모든 유형의 데이터를 저장할 수 있음
public class Tree<T> {
// 루트 노드 필드
private Node<T> root;
// 생성자 -> 필드 초기화
public Tree(T rootData) {
root = new Node<T>();
root.data = rootData;
root.children = new ArrayList<Node<T>>();
}
public static class Node<T> {
private T data;
private Node<T> parent;
private List<Node<T>> children;
}
}
이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리의 목적?
이진탐색 + 연결리스트
이진탐색 : 탐색에 소요되는 시간 복잡도는 O(logN), but 삽입, 삭제가 불가능
연결리스트 : 삽입, 삭제의 시간 복잡도는 O(1), but 탐색하는 시간복잡도가 O(N)
이 두 가지를 합하여 장점을 모두 얻는 것이 '이진 탐색 트리'
즉, 효율적인 탐색 능력을 가지고, 자료의 삽입과 삭제도 가능하게 만들자!
※ 이진 탐색
정렬된 리스트에서 검색 범위를 줄여 나가면서 검색 값을 찾는 알고리즘
- 배열의 중간 값과 검색 값을 비교
- 중간 값이 검색 값과 같으면 탐색 종료 (mid = key)
- 중간 값보다 검색 값이 크다면 중간 값 기준 배열의 오른쪽 구간을 대상으로 다시 이진 탐색 (mid < key)
- 중간 값보다 검색 값이 작다면 중간 값 기준 배열의 왼쪽 구간을 대상으로 다시 이진 탐색 (mid > key)
- 값을 찾거나 간격이 비어있을 때(찾는 값이 없을 때)까지 반복
반복문을 이용하여 이진 탐색
int binarySearch (int arr[], int low, int high, int key) {
while (low <= high) {
int mid = low + (high-low) / 2;
if (arr[mid] == key) // 종료 조건1 검색 성공.
return mid;
else if (arr[mid] > key)
high = mid - 1;
else
low = mid + 1;
}
return -1 ; // 종료 조건2 (low > high) 검색 실패.
}
재귀 함수를 이용하여 이진 탐색
int binarySearch (int arr[], int low, int high, int key) {
if (low > high) // 종료 조건2 검색 실패.
return -1;
int mid = low + (high-low)/2;
if (arr[mid] == key) // 종료 조건1 검색 성공.
return mid;
else if (arr[mid] > key)
return binarySearch(arr, low, mid-1, key);
else
return binarySearch(arr, mid+1, high, key);
}

특징
- 각 노드의 자식이 2개 이하
- 각 노드의 왼쪽 자식은 부모보다 작고, 오른쪽 자식은 부모보다 큼
- 중복된 노드가 없어야 함.
중복이 없어야 하는 이유는?
검색 목적의 자료구조인데, 굳이 중복이 많은 경우의 트리를 사용하여 검색 속도를 느리게 할 필요가 없음
(트리에 삽입하는 것보다, 노드에 count 값을 가지게 하여 처리하는 것이 훨씬 효율적)
이진 탐색 트리의 순회는 '중위 순회(in-order)' 방식을 사용 (왼쪽 - 루트 - 오른쪽)
중위 순회로 정렬된 순서를 읽을 수 있다.
BST 핵심 연산
- 검색
- 삽입
- 삭제
- 트리 생성
- 트리 삭제
※ 검색, 삽입, 삭제의 시간복잡도는 트리의 Depth에 비례
이진 탐색 트리의 탐색 (Search)
다음과 같은 과정을 거친다.
1. 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료한다.
2. 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.
3. 찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행한다.
시간 복잡도 : O(Depth)

탐색 소스코드
TreeNode* search(TreeNode* root, int key) {
if(root == NULL) {
return NULL;
}
if(key == root->key) {
return root;
}
else if(key < root->key) {
search(root->left, key);
}
else if(key > root->key) {
search(root->right, key);
}
}
이진 탐색 트리의 삽입
다음과 같은 과정을 거친다. 탐색과 과정이 비슷하다.
1. 삽입할 값을 루트 노드와 비교해 같다면 오류를 발생시킨다(중복 값 허용 X)
2. 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.
3. 삽입할 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.

void insert(TreeNode** root, int key){
TreeNode* ptr; // 탐색을 진행할 포인터
TreeNode* newNode = (TreeNode*)malloc(sizeof(TreeNode)); // newNode 생성
newNode->key = key;
newNode->left = newNode->right = NULL;
if(*root == NULL){ // 트리가 비어 있을 경우
*root = newNode;
return;
}
ptr = *root; // root 노드부터 탐색 진행
while(ptr){
if(key == ptr->key){ // 중복값
printf("Error : 중복값은 허용되지 않습니다!\n");
return;
}else if(key < ptr->key){ // 왼쪽 서브트리
if(ptr->left == NULL){ // 비어있다면 추가
ptr->left = newNode;
return;
}else{ // 비어있지 않다면 다시 탐색 진행
ptr= ptr->left;
}
}else{ // key > ptr->key 오른쪽 서브트리
if(ptr->right == NULL){ // 비어있다면 추가
ptr->right = newNode;
return;
}else{ // 비어있지 않다면 다시 탐색 진행
ptr = ptr->right;
}
}
}
}
이진 탐색 트리의 삭제 3가지 Case
1. 자식이 없는 leaf 노드일 때 → 그냥 삭제
2. 자식이 1개인 노드일 때 → 지워진 노드에 자식을 올리기
3. 자식이 2개인 노드일 때 → 오른쪽 자식 노드에서 가장 작은 값 or 왼쪽 자식 노드에서 가장 큰 값 올리기
1. leaf 노드의 삭제

- 부모 노드의 자식 노드를 NULL로 만들어 준다.
- 삭제할 노드의 메모리를 해제 해준다.
2. 자식이 1개인 노드 삭제

- 삭제할 노드의 부모노드가 삭제할 노드의 자식노드를 가리키게 한다.
- 삭제할 노드의 메모리를 해제 해준다.
3. 자식이 2개인 노드 삭제
3-1. 삭제할 노드의 왼쪽 서브 트리의 노드 중 값이 가장 큰 노드를 삭제할 노드의 자리에 올린다.
3-2. 삭제할 노드의 오른쪽 서브 트리의 노드 중 값이 가장 작은 노드를 삭제할 노드의 자리에 올린다.

3-1. 삭제할 노드 왼쪽 서브 트리의 가장 큰 자식 노드를 해당 노드의 자리에 올린다.

가장 큰 노드는 자식이 없거나 하나 일 것, 옮길 때 case1이나 2를 사용해서 삭제해주면 된다.
3-2. 삭제할 노드의 오른쪽 서브 트리의 가장 작은 자식 노드를 해당 노드의 자리에 올린다.

int tree_delete(tree *t, int key){
tree *temp = t;
tree *parent = temp;
tree *del;
while(temp->key != key){
parent = temp;
if(temp->key < key){
temp = temp -> right;
}
else
temp = temp -> left;
}
del = temp;
if(temp->left==NULL && temp->right ==NULL){
if(parent->left){
if(temp->key==parent->left->key){
parent->left=NULL; return 1;
}
}
parent->right=NULL;
printf("%d 제거\n",key);
return 1;
}
else if(temp->left!=NULL && temp->right !=NULL){
temp = temp->left;
if(temp->right ==NULL){
del->key = temp->key;
del->left = temp->left;
printf("%d 제거�\n",key);
return 1;
}
while(1){
if(temp->right ==NULL){
del->key = temp->key;
parent->right = temp->left;
printf("%d 제거\n",key);
return 1;
}
else{
parent = temp;
temp= temp->right;
}
}
}
else{
if(temp->right != NULL){
if(parent->left->key == key){
parent->left =temp->right;
}
else{parent->right =temp->right;}
printf("%d 제거\n",key);
return 1;
}
if(temp->left != NULL){
if(parent->left->key == key){
parent->left =temp->left;
}
else{parent->right =temp->left;}
printf("%d 제거\n",key);
return 1;
}
}
}
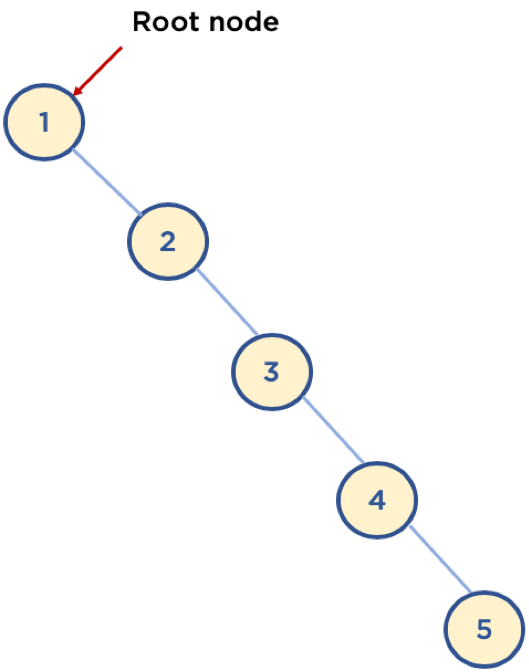
편향된 트리 (정렬된 상태 값을 트리로 만들면 한쪽으로 뻗음)는 시간복잡도가 O(N)이므로 트리를 사용할 이유가 사라짐
→ 이를 바로 잡도록 도와주는 개선된 트리가 AVL Tree, RedBlack Tree
AVL Tree
스스로 균형을 잡는 이진 탐색 트리
특징
- AVL 트리는 이진 탐색 트리의 속성을 가진다.
- 왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1이다.
- 어떤 시점에서 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 높이 차이를 줄인다.
- AVL 트리는 높이를 logN으로 유지하기 때문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN)이다.
Balance Factor(BF)는 왼쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 값이다.
Balance Factor(k) = height(left(k)) - height(right(k))
다음은 AVL 트리의 예이다. BF가 -1 과 +1 사이에 있음을 알 수 있다.

Rotation (회전)
AVL 트리는 이진 탐색 트리이기 때문에 모든 작업은 이진 탐색 트리에서 사용하는 방식으로 수행됨
검색 및 순회 연산은 BF를 변경하지 않지만 삽입 및 삭제에서는 BF가 변경될 수 있다.
삽입 및 삭제 시 불균형 상태(BF가 -1, 0, 1이 아닌 상태)가 되면 AVL 트리는 불균형 노드를 기준으로 서브트리의 위치를 변경하는
rotation 작업을 수행하여 트리의 균형을 맞춘다.
삽입 및 삭제 시 노드들의 배열에 따라 4가지 불균형(LL, RR, LR, RL)이 발생할 수 있으며
각 상황마다 rotation 방향을 달리하여 트리의 균형을 맞출 수 있다.
우회전(Right Rotation)
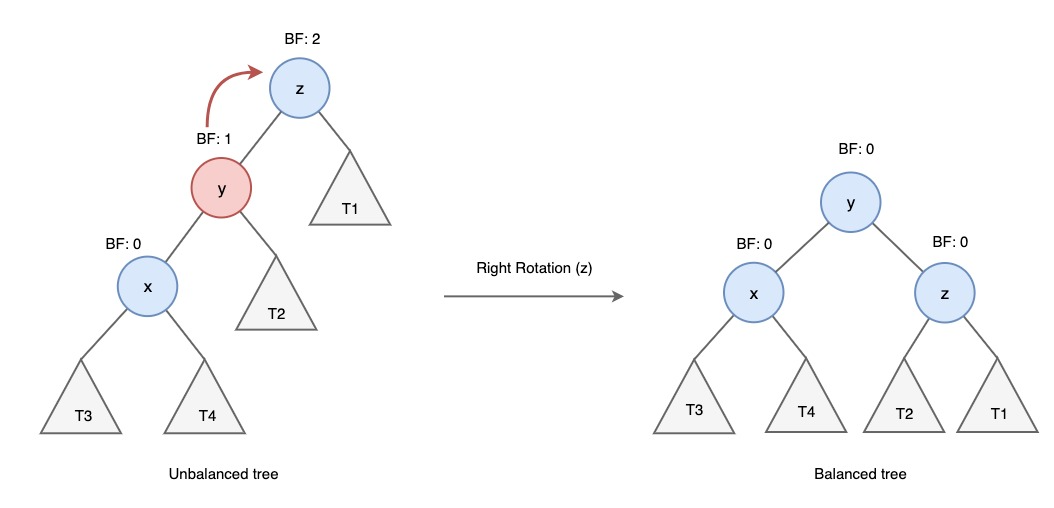
1. y노드의 오른쪽 자식 노드를 z노드로 변경한다.
2. z노드의 왼쪽 자식 노드를 y노드 오른쪽 서브트리(T2)로 변경한다.
→ y노드가 새로운 루트 노드가 된다.
좌회전(Left Rotation)

1. y노드의 왼쪽 자식 노드를 z노드로 변경한다.
2. z노드의 오른쪽 자식 노드를 y노드 왼쪽 서브트리(T2)로 변경한다.
→ y노드가 새로운 루트 노드가 된다.
LL(Left Left) Case

RR(Right Right) Case

LR(Left Right) Case

여기서부터는 살짝 다르다.
LR 문제는 좌측이 비대한 문제와 우측이 비대한 문제를 동시에 가지고 있다.
따라서, 이 문제를 해결하기 위해선 우측 비대 문제를 먼저 해결해야 한다.
→ 좌회전부터 먼저 수행 → LL 케이스가 됨 → 우회전 시켜줌

RL(Right Left) Case

참고:
https://gyoogle.dev/blog/computer-science/data-structure/Binary%20Search%20Tree.html
이진탐색트리 (Binary Search Tree) | 👨🏻💻 Tech Interview
이진탐색트리 (Binary Search Tree) 이진탐색트리의 목적은? 이진탐색 + 연결리스트 이진탐색 : 탐색에 소요되는 시간복잡도는 O(logN), but 삽입,삭제가 불가능 연결리스트 : 삽입, 삭제의 시간복잡도는
gyoogle.dev
https://code-lab1.tistory.com/10
[자료구조] 이진탐색트리(Binary Search Tree)의 개념, 이해 | C언어 이진탐색트리 구현
이진탐색트리(Binary Search Tree)이란? 이진탐색트리란 다음과 같은 특징을 갖는 이진트리를 말한다. ( #이진트리 - 각 노드의 자식 노드가 최대 2개인 트리) 1. 각 노드에 중복되지 않는 키(key)가 있다
code-lab1.tistory.com
https://kis6473.tistory.com/30
[BST] 이진 탐색 트리 알고리즘을 이용한 데이터 삽입,삭제(C언어코드포함)
댓글로 소스 문의가 많아서 파일로 첨부했습니다. 저도 학교 수업 들으면서 처음 짜본 코드라 부족하고, 틀린 부분도 있을 수 있지만 도움이 되면 좋겠네요 이진 탐색 트리란? (BST) 이진 탐색 트
kis6473.tistory.com
'CS 공부 > Data Structure' 카테고리의 다른 글
| [Stack] 스택 (0) | 2024.02.06 |
|---|---|
| [7주차] Data Structure (B-Tree, B+Tree) (1) | 2023.12.26 |
| [6주차] Data Structure (해시 함수, 트라이) (1) | 2023.11.26 |
| [4주차] Data Structure 2/4 (스택과 큐, 힙) (3) | 2023.10.13 |
| [3주차] Data Structure 1/4 (배열, 연결 리스트) (1) | 2023.10.13 |




