| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 우선순위 큐
- Timsort
- 파싱
- 팀정렬
- 해시함수
- 프로그래머스
- collections.sort
- LinkedList
- 퀵정렬
- 15552번
- 분할정복
- heap
- 이진트리탐색
- 삽입정렬
- 스택
- stack
- 큐
- 코딩테스트
- 힙
- 거품정렬
- divide and conquer
- 연결리스트
- 코테준비
- 트라이
- 코테
- 선택정렬
- MSA
- 스터디
- 자료구조
- 백준
- Today
- Total
Little bIT awesome
[6주차] Data Structure (해시 함수, 트라이) 본문
해시 함수
데이터를 효율적으로 관리하기 위해, 임의의 길이 데이터를 고정된 길이의 데이터로 매핑하는 것.
해시 함수를 구현하여 데이터 값을 해시 값으로 매핑한다.
이 때, 매핑 전 원래 데이터의 값을 Key
매핑 후 데이터의 값을 hash value(해시 값)
매핑하는 과정 자체를 hashing(해싱) 이라고 한다.
해시 함수를 구현하여 데이터 값을 해시 값으로 매핑한다.
collision
Lee → 해싱함수 → 5
Kim → 해싱함수 → 3
Park → 해싱함수 → 2
...
Chun → 해싱함수 →5 // Lee 해싱값과 충돌

해시함수는 해쉬값의 개수보다 대개 많은 키값을 해쉬값으로 변환(many-to-one 대응)하기 때문에
해시함수가 서로 다른 두 개의 키에 대해 동일한 해시값을 내는 해쉬충돌(collision)이 발생하게 된다.
해시 테이블
해시함수를 사용하여 키를 해시값으로 매핑하고, 이 해시값을 index 혹은 주소로 삼아 데이터의 값을 키와 함께 저장하는 자료구조.
이 때, 데이터가 저장되는 곳을 버킷(bucket) 또는 슬롯(slot)이라고 한다. 해시 테이블의 기본 연산은 삽입, 삭제, 탐색.

| Index(Hash Value) | Data |
| 01 | (Lisa Smith, 521-8976) |
| 02 | (John Smith, 521-1234) |
| ... | ... |
키와 전체 개수가 동일한 크기의 버킷을 가진 해시테이블을 Direct-address table 이라고 한다.

키 개수와 해시테이블의 크기가 동일하기 때문에 해시충돌 문제가 발생하지 않는다.
하지만, 전체 키(universe of key)가 사용하는 실제 키(actual key)보다 훨씬 많기 때문에 메모리 효율성이 떨어진다.
보통의 경우 Direct-address table 보다는 "해시테이블의 크기(m)가 실제 사용하는 키 개수(n)보다 적은 해시테이블"을 운용한다.
이 때, n/m을 load factor(α)라고 한다. 해시 테이블의 한 버킷에 평균 몇 개의 키가 매핑되는가를 나타내는 지표로 사용된다.
Direct-address table의 load factor는 1 이하, 1보다 클 경우 해시 충돌 문제가 발생한다.
해시 테이블의 장점
- 적은 리소스으로 많은 데이터를 효율적으로 관리할 수 있다.
하드디스크, 클라우드 등에 존재하는 무한에 가까운 데이터(키)들을 유한한 개수의 해시값으로 매핑하면
작은 크기의 캐쉬 메모리로도 프로세스를 관리할 수 있게 된다. - index를 알면 해시테이블의 크기에 관계없이 데이터에 빠르게 접근할 수 있다.
해시함수는 언제나 동일한 해시값을 리턴
index는 계산이 간단한 함수로 작동하기 때문에 매우 효율적이다.
데이터 접근(삽입, 삭제, 탐색)의 시간복잡도 O(1) (이진탐색트리는 O(logN), 배열의 경우 메모리를 미리 할당해 둬야 함) - 보안 분야에서 널리 사용된다.
키와 해시값 사이에 직접적인 연관이 없기 때문에 해시값만 가지고는 키를 온전히 복원하기 어려움
길이가 서로 다른 입력 데이터(키)에 대해서 일정한 길이의 출력을 만들 수 있어 '데이터 축약'의 기능도 수행
충돌 문제 해결
1. Chaning (체이닝)
한 버킷당 들어갈 수 있는 엔트리의 수에 제한을 두지 않음으로써 모든 자료를 해시테이블에 담는 방식
연결리스트 자료 구조를 사용하여 체인처럼 노드를 추가하여 다음 노드를 가리키는 방식으로 구현
제한 없이 계속 연결이 가능하다는 장점이 있으나 메모리 문제를 야기할 수 있다.
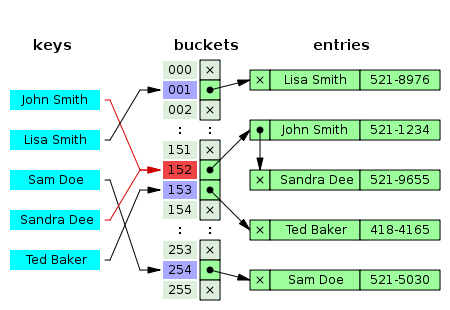
2. Open Addressing
한 버킷당 들어갈 수 있는 엔트리가 하나뿐인 해시테이블, 메모리 문제가 발생하지 않으나 해시충돌이 생길 수 있다.
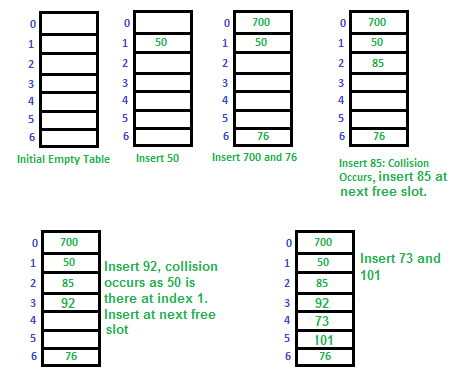
예를 들어, 해시함수를 '키값을 7으로 나눈 나머지' 정의했다고 하자.
85를 7로 나눈 나머지는 1인데, 이미 50이 버킷에 들어있으므로 다음 버킷에 저장해 줌
해시 함수로 얻은 주소가 아닌 다른 주소에 데이터를 저장할 수 있도록 허용하는 방색
해당 키 값에 저장되어 있으면 다음 주소에 저장
2-1. 선형 탐사
Open Addressing의 가장 간단한 방식.
최초 해시값에 해당하는 버킷에 다른 데이터가 저장되어 있으면 해당 해시값에서
고정 폭(앞의 예시는 1칸)만큼 옮겨 다음 해시값에 해당하는 버킷에 저장한다.
여기에도 데이터가 있으면 고정폭만큼을 또 옮겨 엑세스

특정 해시값 주변 버킷이 모두 채워져 있는 primary clustering 문제에 취약함.
2-2. 제곱 탐사
고정 폭으로 이동하는 선형 탐사와 달리 그 폭이 제곱수로 늘어난다.
임의의 키값에 해당하는 데이터에 액세스할 때 충돌이 일어나면 1^2칸을 옮기고
여기에서도 충돌이 일어나면 2^2칸, 그 다음엔 3^2칸 옮기는 방식

여러 개의 서로 다른 키들이 동일한 초기 해시값을 갖는 secondary clustering에 취약.
초기 해시값이 같으면 다음 탐사 위치 또한 동일하기 때문에 효율성이 떨어짐
3. 이중 해싱
2개의 해시함수를 준비해서 하나는 최초의 해시값을 얻을 때, 또 다른 하나는 해시충돌이 일어났을 때 담사 이동폭을 얻기 위해 사용한다.
최초 해시값이 같더라도 탐사 이동폭이 달라지고, 탐사 이동폭이 같더라도 최초 해시값이 달라져
primary clustering, secondary clustering을 모두 완화할 수 있다.
- 해시값을 반환해주는 ℎ1ℎ1을 ‘3으로 나눈 나머지’, 탐사 이동폭을 결정해주는 ℎ2ℎ2를 ‘5로 나눈 나머지’라고 둡시다. 예컨대 키가 3, 6인 데이터의 최초 해시값은 모두 0이 됩니다. 하지만 키가 3인 데이터의 탐사이동폭은 3, 6인 데이터의 이동폭은 1로 달라집니다. 반대로 키가 6, 11인 데이터의 탐사이동폭은 모두 1이 됩니다. 하지만 키가 6인 데이터의 최초 해시값은 0, 11은 2로 달라집니다.
https://ratsgo.github.io/data%20structure&algorithm/2017/10/25/hash/
해싱, 해시함수, 해시테이블 · ratsgo's blog
이번 글에서는 해싱(hashing)에 대해 살펴보도록 하겠습니다. 이 글은 고려대 김선욱 교수님 강의와 위키피디아, 그리고 스택오버플로우와 고니 님의 블로그를 참고해 정리하였음을 먼저 밝힙니
ratsgo.github.io
트라이(Trie)
문자열에서 검색을 빠르게 도와주는 자료구조
"여러 개의 문자열을 가지고 있을 때, 어떤 문자열이 그 문자열 중 하나인지 알아내는 과정"
정수형에서 이진탐색트리를 사용하면 시간복잡도 O(logN)
하지만 문자열에서 적용했을 때, 문자열 최대 길이가 M이면 O(M*logN)이 된다.
두 문자열을 비교하기 위해서 문자열의 길이만큼 시간이 걸리기 때문
트라이를 활용하면? → O(M)으로 문자열 검색이 가능하다.
작동원리
다음 그림은 문자열 집합 {"rebro", "replay", "hi" , "high", "algo"} 를 트라이로 구현한 것이다.

트라이는 한 문자열에서 다음에 나오는 문자가 현재 문자의 자식 노드가 된다.
빨간색으로 나타낸 리프 노드는 문자열의 끝을 의미한다.
문자열 탐색을 위해서는 다음 글자에 해당하는 노드를 타고 따라가면 된다. -> O(M)만큼의 시간이 걸림!
루트에서부터 내려가는 경로에서 만나는 글자들을 모으면, 찾고자하는 문자열의 접두사를 구할 수 있다.
ex) "rebro"를 찾는다고 해보자
r → re → reb → rebr → rebro 순으로 탐색되므로 "rebro"의 모든 접두사들이 다 구해진다.
장점
문자열을 빠르게 찾을 수 있다.
문자열을 추가하는 경우에도 문자열의 길이만큼 노드를 따라가서 추가하면 되기 때문에 문자열의 추가와 탐색이 모두 O(M)만에 가능하다.
단점
필요한 메모리의 크기가 너무 크다
문자열이 모두 알파벳 소문자로만 이루어진 경우라고 해도 1 depth에 a~z까지 26개의 공간이 필요하다.
'CS 공부 > Data Structure' 카테고리의 다른 글
| [Stack] 스택 (0) | 2024.02.06 |
|---|---|
| [7주차] Data Structure (B-Tree, B+Tree) (1) | 2023.12.26 |
| [5주차] Data Structure 3/4 (트리 & 이진 탐색 트리) (1) | 2023.11.19 |
| [4주차] Data Structure 2/4 (스택과 큐, 힙) (3) | 2023.10.13 |
| [3주차] Data Structure 1/4 (배열, 연결 리스트) (1) | 2023.10.13 |




